画像から円を検出し、色でグループ化して最長経路を繋げてみる
Contents
概要
1枚の画像から円を検出して、最長経路を探索するプログラムです。
理由は特にないですが、3つ以上繋がっている時だけ経路探索をしたいと思います。
※決してツムツムの自動化ロジックの一部ではありません。あくまで円を検出して経路を探索するプログラムです。
プログラムの内容と説明
サンプル画像
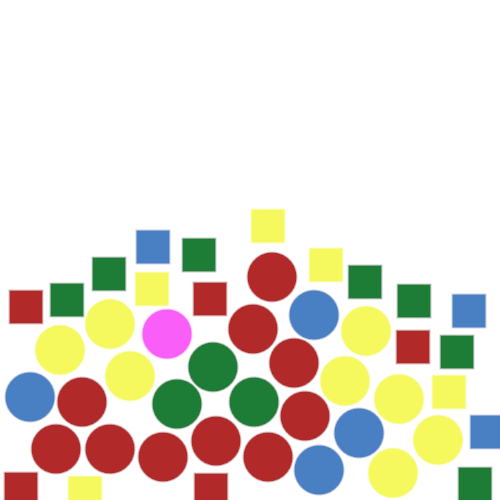
ツムツムの自動化を実装するわけではないので、自分で円が繋がっている感じの画像を用意します。本記事では以下の画像をサンプルとしています。ダウンロードして使ってください。
プログラム本体
import cv2
import numpy as np
from PIL import Image
import math
from graphillion import GraphSet as gs
import collections
# HSVの許容範囲(同一グループ判定に使用)
HUE_MARGIN = 50
SATURATION_MARGIN = 50
VALUE_MARGIN = 50
# ヒストグラム類似度の閾値(同一グループ判定に使用)
HISTOGRAM_SIMILARITY_THRESHOLD = 0.7
# 経路探索範囲(円同士が繋がっていると判定する距離)
SEARCH_RANGE = 70
# 円中心点からの矩形切り取り範囲(色情報の平均化に使用)
CUT_RECTANGLE = 10
def main():
img = cv2.imread("./sample.png")
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# ハフ変換での円検出
circles = cv2.HoughCircles(gray, cv2.HOUGH_GRADIENT, dp=1, minDist=10, param1=25, param2=40, minRadius=10, maxRadius=40)
# 円を発見した場合のみ処理を行う
if circles is not None:
circles = np.uint16(np.around(circles))
p_img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
p_img = Image.fromarray(p_img)
circle_groups = []
circle_id = 1
for i, circle in enumerate(circles[0, :]):
# 切り取り範囲を取得
left = max(0, circle[0] – circle[2] + CUT_RECTANGLE)
upper = max(0, circle[1] – circle[2] + CUT_RECTANGLE)
right = min(p_img.width, circle[0] + circle[2] – CUT_RECTANGLE)
lower = min(p_img.height, circle[1] + circle[2] – CUT_RECTANGLE)
# 円の中心から矩形範囲で切り取り
cropped_img = p_img.crop((left, upper, right, lower))
cropped_img_arr = np.array(cropped_img)
# ヒストグラムを計算し平坦化
hist = cv2.calcHist([cropped_img_arr], [0, 1, 2], None, [8, 8, 8], [0, 256, 0, 256, 0, 256])
hist = cv2.normalize(hist, hist).flatten()
# HSVに変換し平均値を取得
hsv = cv2.cvtColor(cropped_img_arr, cv2.COLOR_RGB2HSV)
hsv_avg = np.average(np.average(hsv, axis=0), axis=0)
# 円情報をグループ化
grouped = False
for group in circle_groups:
ref_hist = group['hist']
similarity = cv2.compareHist(hist, ref_hist, cv2.HISTCMP_CORREL)
ref_hsv_avg = group['hsv']
# ヒストグラムの類似度とHSVの許容範囲を比較
if similarity > HISTOGRAM_SIMILARITY_THRESHOLD and \
abs(hsv_avg[0] – ref_hsv_avg[0]) < HUE_MARGIN and \
abs(hsv_avg[1] – ref_hsv_avg[1]) < SATURATION_MARGIN and \
abs(hsv_avg[2] – ref_hsv_avg[2]) < VALUE_MARGIN:
group['circles'].append({
'circle_id': circle_id,
'position': (circle[0], circle[1]),
'radius': circle[2],
'select': False
})
grouped = True
break
# 新規グループの場合
if not grouped:
circle_groups.append({
'circles': [{
'circle_id': circle_id,
'position': (circle[0], circle[1]),
'radius': circle[2],
'select': False
}],
'hist': hist,
'hsv': hsv_avg
})
circle_id += 1
# 最長経路リストを取得
SelectionRoute = calcRoute(circle_groups)
# 最長経路リストを描画
for RouteStart in SelectionRoute:
# 始点、終点(要素をずらした始点リストコピー)リストを作成する
RouteEnd = RouteStart[1:] + RouteStart[:1]
RouteStart.pop()
RouteEnd.pop()
# 矢印の描画
for i, _ in enumerate(RouteStart):
cv2.arrowedLine(img, RouteStart[i], RouteEnd[i], (0, 0, 0), 2)
for circle in circles[0, :]:
# 円周を描画する
cv2.circle(img, (circle[0], circle[1]), circle[2], (0, 165, 255), 5)
# 中心点を描画する
cv2.circle(img, (circle[0], circle[1]), 2, (0, 0, 255), 3)
# 画像の生成
cv2.imwrite("result.png", img)
# 画像表示
cv2.imshow("Image", img)
# キー入力待ち(画像が表示される)
cv2.waitKey()
# 距離計算関数
def distance(pos1, pos2):
return math.sqrt((int(pos1[0]) – int(pos2[0])) ** 2 + (int(pos1[1]) – int(pos2[1])) ** 2)
'''
処理名: 経路探索関数
概要 : グループごとに最長経路を最大で1つ探索しリストを作成
引数1 : グループ情報(全量)
'''
def calcRoute(circle_groups):
SelectionRoute = []
# グループごとにループ
for group in circle_groups:
# 辺の集合「(1,2)(2,3)」を入れる
retData = []
# 辺の集合を作成する関数をコール
# 各グループの各円を基点にして処理を行う
retData = []
for circle in group['circles']:
_retData = []
distanceDataGet(group['circles'], circle['circle_id'], _retData)
# 保持している辺集合よりも要素が多い場合、保持
if len(retData) < len(_retData):
retData = _retData
# 辺の集合最大値が2未満なら次グループへ
if len(retData) < 2:
continue
# ユニバースの作成(retDataがそのままユニバースとして使用可能な形式)
universe = retData
# グラフセットの作成
gs.set_universe(universe)
# 最長経路探索を行う
maxPath = []
for startPoinst in tuple(set(sum(retData, ()))):
for endPoint in tuple(set(sum(retData, ()))):
if startPoinst == endPoint:
continue
# 始点と終点を仮設定
paths = gs.paths(startPoinst, endPoint)
# 仮の最長経路を取得
thisMaxPath = next(paths.max_iter())
# 仮の最長経路と保持している最長経路の長い方を保持
if len(maxPath) < len(thisMaxPath):
maxPath = thisMaxPath
s = startPoinst
e = endPoint
# 選択経路変換
# ※maxPathは辺の集合であり、実際に繋ぐ順番と異なる
# そのため始点からの順番で選択順番リストを作る
# リストはpositionを保持、その方が描画および選択する際に楽
tmpRoute = []
limit = len(maxPath)
while len(tmpRoute) < limit:
for c in range(len(maxPath)):
#辺の集合体のため、双方から経路を繋いでい
if maxPath[c][0] == s:
tmpRoute.append([c for c in group['circles'] if c['circle_id'] == s][0]['position'])
s = maxPath[c][1]
maxPath.pop(c)
break
if maxPath[c][1] == s:
tmpRoute.append([c for c in group['circles'] if c['circle_id'] == s][0]['position'])
s = maxPath[c][0]
maxPath.pop(c)
break
# 終点のpositionを保持
tmpRoute.append([c for c in group['circles'] if c['circle_id'] == e][0]['position'])
# 選択経路に追加
SelectionRoute.append(tmpRoute)
return SelectionRoute
'''
処理名: 範囲内データ抽出関数
概要 : 再帰呼び出しで繋がっているcircle_idタプルリストを作成
引数1 : グループ内円情報(全量)
引数2 : 基点の円情報
引数3 : 繋がり情報(タプルのリスト)
'''
def distanceDataGet(circles, circle_id, retData):
# circle_idが一致する基点データを抽出
circle = [c for c in circles if c['circle_id'] == circle_id]
# 基点データを選択済とする
circle[0]['select'] = True
# 基点データとの距離が近い かつ 未選択のグループを取得
nonSelectedGroup = [c for c in circles if not c['select'] and distance(circle[0]['position'], c['position']) <= SEARCH_RANGE ]
for nonSelectedCircle in nonSelectedGroup:
# 範囲内データに追加
if not (circle_id, nonSelectedCircle['circle_id']) in retData and not (nonSelectedCircle['circle_id'], circle_id) in retData:
retData.append((circle_id, nonSelectedCircle['circle_id']))
# 次の基点を指定して再帰呼び出し
distanceDataGet(circles, nonSelectedCircle['circle_id'], retData)
# 基点データの選択を解除
circle[0]['select'] = False
return retData
if __name__ == "__main__":
main()処理結果
上記プログラムを実行した結果は以下となります。
画像左の黄色3個はつながっていませんが、これはグループ内の最大経路を取得する仕様にしているためです。右の黄色5個が黄色グループとしては最長経路のため、そちらを繋いだ状態となっています。
グループ自体を分ければ、左の黄色3個も経路を探索することが可能です。
処理の解説
円の検出
# ハフ変換での円検出
circles = cv2.HoughCircles(gray, cv2.HOUGH_GRADIENT, dp=1, minDist=10, param1=25, param2=40, minRadius=10, maxRadius=40)一番の肝である円の検出です。検出用のパラメータはサンプル画像に最適化しているため、使用する画像を変更する場合には各自調整してください。
HoughCirclesの各引数の設定は以下のサイト様の説明が分かりやすいです。
https://shikaku-mafia.com/cv2-houghcircles/円のグループ化
円のグループ化の処理です。
円の中心点から指定範囲の画像を切り抜き、切り抜いた画像のヒストグラムとHSVでのグルーピングを行ってみました。
RGBの許容値等の判定も使用すればもう少し精度は上がりますが、少しのずれで別グループとみなされるため、これくらいがちょうどいいかもしれません。
for i, circle in enumerate(circles[0, :]):
# 切り取り範囲を取得
left = max(0, circle[0] – circle[2] + CUT_RECTANGLE)
upper = max(0, circle[1] – circle[2] + CUT_RECTANGLE)
right = min(p_img.width, circle[0] + circle[2] – CUT_RECTANGLE)
lower = min(p_img.height, circle[1] + circle[2] – CUT_RECTANGLE)
# 円の中心から矩形範囲で切り取り
cropped_img = p_img.crop((left, upper, right, lower))
cropped_img_arr = np.array(cropped_img)
# ヒストグラムを計算し平坦化
hist = cv2.calcHist([cropped_img_arr], [0, 1, 2], None, [8, 8, 8], [0, 256, 0, 256, 0, 256])
hist = cv2.normalize(hist, hist).flatten()
# HSVに変換し平均値を取得
hsv = cv2.cvtColor(cropped_img_arr, cv2.COLOR_RGB2HSV)
hsv_avg = np.average(np.average(hsv, axis=0), axis=0)
# 円情報をグループ化
grouped = False
for group in circle_groups:
ref_hist = group['hist']
similarity = cv2.compareHist(hist, ref_hist, cv2.HISTCMP_CORREL)
ref_hsv_avg = group['hsv']
# ヒストグラムの類似度とHSVの許容範囲を比較
if similarity > HISTOGRAM_SIMILARITY_THRESHOLD and \
abs(hsv_avg[0] – ref_hsv_avg[0]) < HUE_MARGIN and \
abs(hsv_avg[1] – ref_hsv_avg[1]) < SATURATION_MARGIN and \
abs(hsv_avg[2] – ref_hsv_avg[2]) < VALUE_MARGIN:
group['circles'].append({
'circle_id': circle_id,
'position': (circle[0], circle[1]),
'radius': circle[2],
'select': False
})
grouped = True
break
# 新規グループの場合
if not grouped:
circle_groups.append({
'circles': [{
'circle_id': circle_id,
'position': (circle[0], circle[1]),
'radius': circle[2],
'select': False
}],
'hist': hist,
'hsv': hsv_avg
})
circle_id += 1最長経路の探索
最長経路の探索にはgraphillionというライブラリを使用します。
簡単に説明すると、こことここが繋がってるよって情報をまとめておくと、経路探索を簡単かつ高速で行ってくれるライブラリです。
繋がりはタプルで表現します。
[(1, 2), (2, 3)]というタプルリストがあったとしたら、1と2、2と3が繋がっているが、1と3が繋がっていない状態を表現したものとなります。
もし1と3も繋がっている場合は[(1, 2), (2, 3), (1, 3)]のように表します。
最長経路の探索には以下のサイト様を参考にしました。
https://tech.mobilefactory.jp/entry/2018/12/20/180000範囲内データ抽出関数
上記の繋がりを表したタプルの生成関数です。
基点から順に選択状態を更新していき、近いものを探索して再度それを基点としてまた当関数をコールしています。
'''
処理名: 範囲内データ抽出関数
概要 : 再帰呼び出しで繋がっているcircle_idタプルリストを作成
引数1 : グループ内円情報(全量)
引数2 : 基点の円情報
引数3 : 繋がり情報(タプルのリスト)
'''
def distanceDataGet(circles, circle_id, retData):
# circle_idが一致する基点データを抽出
circle = [c for c in circles if c['circle_id'] == circle_id]
# 基点データを選択済とする
circle[0]['select'] = True
# 基点データとの距離が近い かつ 未選択のグループを取得
nonSelectedGroup = [c for c in circles if not c['select'] and distance(circle[0]['position'], c['position']) <= SEARCH_RANGE ]
for nonSelectedCircle in nonSelectedGroup:
# 範囲内データに追加
if not (circle_id, nonSelectedCircle['circle_id']) in retData and not (nonSelectedCircle['circle_id'], circle_id) in retData:
retData.append((circle_id, nonSelectedCircle['circle_id']))
# 次の基点を指定して再帰呼び出し
distanceDataGet(circles, nonSelectedCircle['circle_id'], retData)
# 基点データの選択を解除
circle[0]['select'] = False
return retData経路探索用関数
範囲内データ抽出関数を用いて、最長経路の探索を行う関数です。
同一グループ内で最長経路を探す仕様となっています。
'''
処理名: 経路探索関数
概要 : グループごとに最長経路を最大で1つ探索しリストを作成
引数1 : グループ情報(全量)
'''
def calcRoute(circle_groups):
SelectionRoute = []
# グループごとにループ
for group in circle_groups:
# 辺の集合「(1,2)(2,3)」を入れる
retData = []
# 辺の集合を作成する関数をコール
# 各グループの各円を基点にして処理を行う
retData = []
for circle in group['circles']:
_retData = []
distanceDataGet(group['circles'], circle['circle_id'], _retData)
# 保持している辺集合よりも要素が多い場合、保持
if len(retData) < len(_retData):
retData = _retData
# 辺の集合最大値が2未満なら次グループへ
if len(retData) < 2:
continue
# ユニバースの作成(retDataがそのままユニバースとして使用可能な形式)
universe = retData
# グラフセットの作成
gs.set_universe(universe)
# 最長経路探索を行う
maxPath = []
for startPoinst in tuple(set(sum(retData, ()))):
for endPoint in tuple(set(sum(retData, ()))):
if startPoinst == endPoint:
continue
# 始点と終点を仮設定
paths = gs.paths(startPoinst, endPoint)
# 仮の最長経路を取得
thisMaxPath = next(paths.max_iter())
# 仮の最長経路と保持している最長経路の長い方を保持
if len(maxPath) < len(thisMaxPath):
maxPath = thisMaxPath
s = startPoinst
e = endPoint
# 選択経路変換
# ※maxPathは辺の集合であり、実際に繋ぐ順番と異なる
# そのため始点からの順番で選択順番リストを作る
# リストはpositionを保持、その方が描画および選択する際に楽
tmpRoute = []
limit = len(maxPath)
while len(tmpRoute) < limit:
for c in range(len(maxPath)):
#辺の集合体のため、双方から経路を繋いでい
if maxPath[c][0] == s:
tmpRoute.append([c for c in group['circles'] if c['circle_id'] == s][0]['position'])
s = maxPath[c][1]
maxPath.pop(c)
break
if maxPath[c][1] == s:
tmpRoute.append([c for c in group['circles'] if c['circle_id'] == s][0]['position'])
s = maxPath[c][0]
maxPath.pop(c)
break
# 終点のpositionを保持
tmpRoute.append([c for c in group['circles'] if c['circle_id'] == e][0]['position'])
# 選択経路に追加
SelectionRoute.append(tmpRoute)
return SelectionRoute