モンティ・ホール問題を実践してみる

はじめに

今回は以前より試してみたかったモンティ・ホール問題をプログラミングしてみます。「終物語」や「嘘食い」などアニメやマンガでも登場する機会もあったので、知っている方も多いと思います。

モンティ・ホール問題とは

調べれば解説や説明がたくさん出てくると思うので、概要だけ載せておきます。

「プレーヤーの前に閉まった3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろには、はずれを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。プレーヤーが1つのドアを選択した後、司会のモンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。

ここでプレーヤーは、最初に選んだドアを、残っている開けられていないドアに変更してもよいと言われる。プレーヤーはドアを変更すべきだろうか？」

1990年9月9日発行、ニュース雑誌 Parade にて、マリリン・ボス・サヴァントが連載するコラム「マリリンにおまかせ」において上記の読者投稿による質問に「正解は『ドアを変更する』である。なぜなら、ドアを変更した場合には景品を当てる確率が2倍になるからだ」と回答した。すると直後から、読者からの「彼女の解答は間違っている」との約1万通の投書が殺到し、本問題は大議論に発展した。

Wikipediaより引用

実践

システムを作る

今回はC#.Netでフォーム型アプリケーションを作成しました。
あたりの数や、取り除く値、実行回数を変更できるようにしてあります。

選択を変える場合と変えない場合で、どちらがいいのか検証してみます。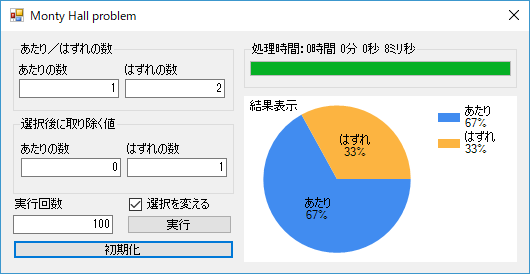

動作させてみる

基本となる3つの中で1つだけがあたり、選択後にはずれを1つ取り除くケース。
取り除いた後に選択を変えない場合を実行してみます。
実行回数は100万回を数回実行します。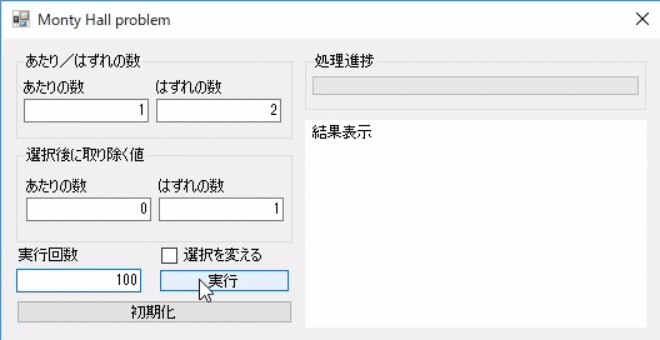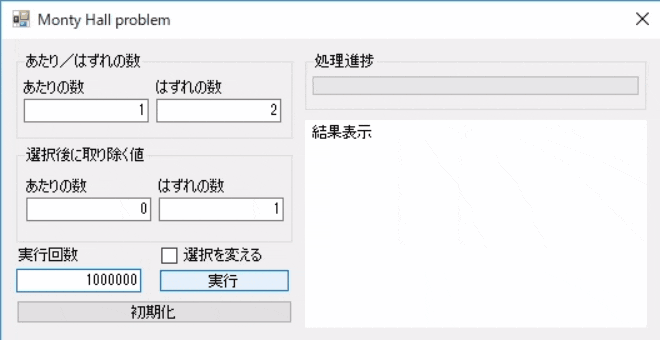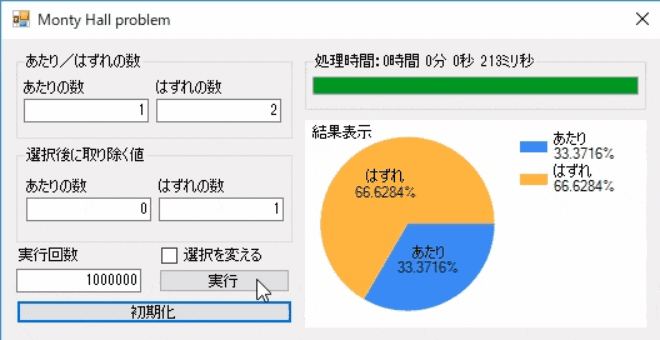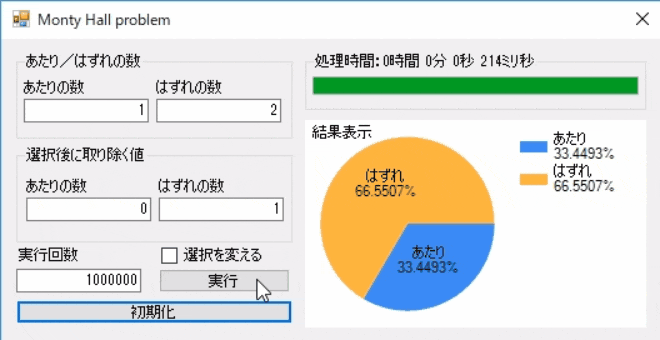
3分の1から選択を変えていないので、当たる確率もほぼ33.333％で想定通りの値ですね。

次は、同じ条件で選択を変えてみます。
想定では変更する前の2倍、ほぼ66.666％となる予定です。

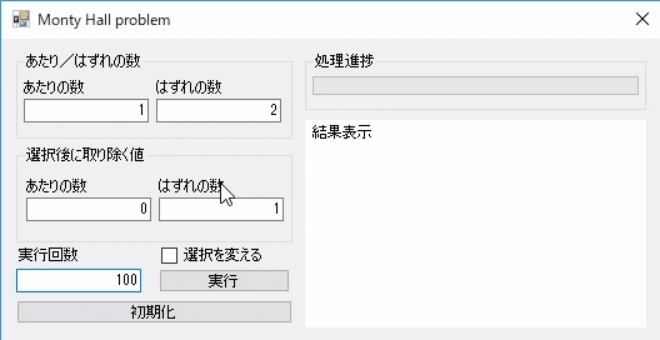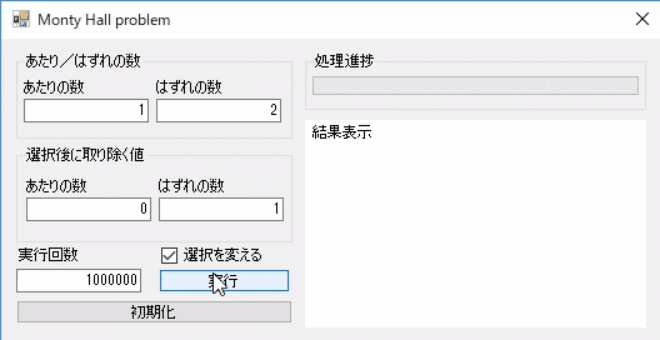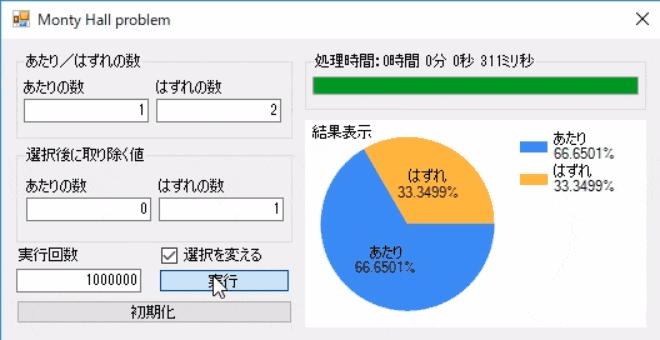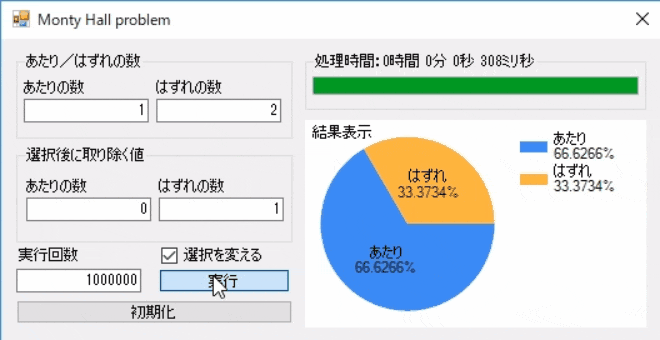
想定通り、ほぼ66.666％となりました。

わかったこと

はずれを取り除いた後の形が「あたり1つ、はずれ1つ」という形になるということは、選択を変えた場合、最初に選択したものと結果が反転するということがわかりました。
はずれを引く確率が多ければ多いほど、選択を変えることの恩恵が大きくなります。

直観的に理解しやすくするためにはずれが2つでなく、はずれが99個だった場合というものがありますが、この例では結果が反転していることがよくわかります。

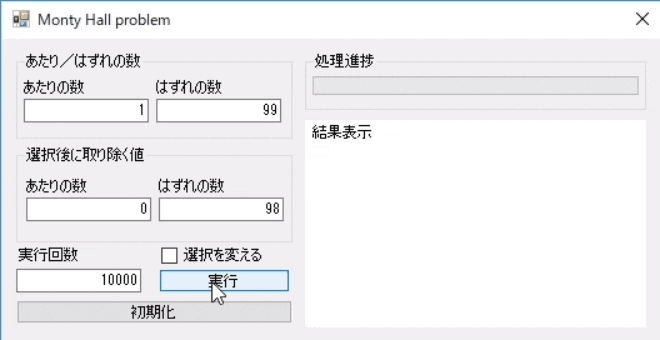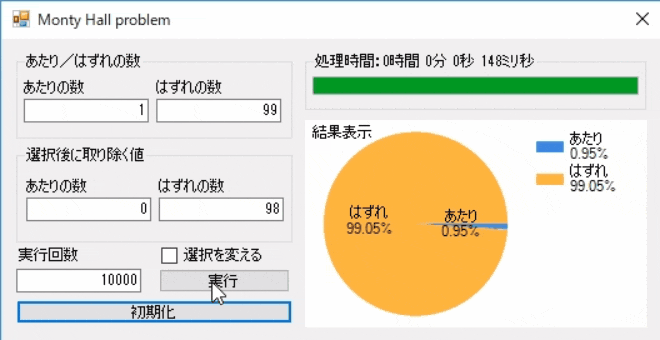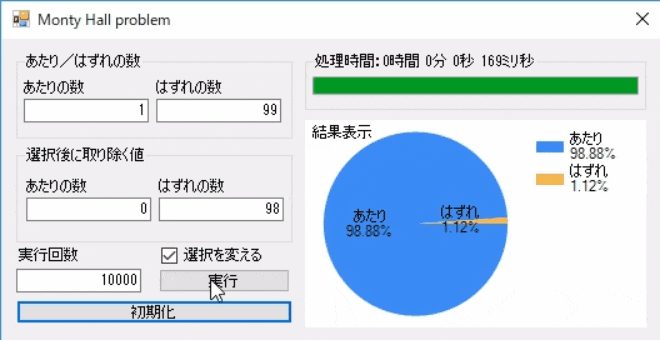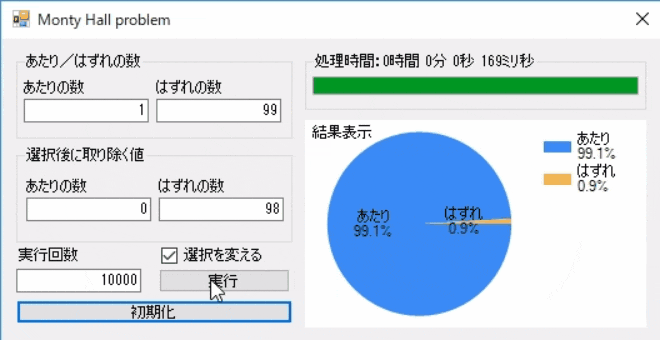
一応、はずれが99個ケースも実践しておきます。
少し処理が重いので試行回数は1万回を数回にします。

その他のケース

あたりを複数用意し、あたりを取り除くケースや、取り除いた後にあたりとはずれが複数ずつ残るケースなど、試せるケースはたくさんあります。

特殊ルール付けを行った天使モンティや、悪魔モンティというものもありますので気になった方は是非調べてみてください。

ソースや実行ファイル

ブログを書くにあたって作成したプログラムを残しておきます。

＜注意＞
・数値の整合性チェック等は行っていませんので、あり得ない組み合わせで実行するとエラーとなります。
・ソースも冗長な部分が多数ありますので、参考にはなりません。

 

C#,その他

Posted by marimo